Luận cứ phương pháp nghiên cứu học máy dự đoán ô nhiễm môi trường
Có rất nhiều nguyên nhân liên quan đến ô nhiễm, nguyên nhân chính liên quan đến ô nhiễm không khí là đốt nhiên liệu, nông nghiệp, khí thải từ các nhà máy và ngành công nghiệp, sưởi ấm khu dân cư và thiên tai.
Trước các vấn đề ô nhiễm môi trường ngày càng nghiêm trọng, các nhà khoa học đã tiến hành nhiều nghiên cứu liên quan, trong các nghiên cứu đó, việc dự báo ô nhiễm không khí, góp phần phát triển kinh tế bền vững là điều tối quan trọng. Do đó, với kiến thức đầy đủ về các vấn đề phát sinh ô nhiễm ngày càng tăng, tầm quan trọng của việc dự báo chính xác mức độ ô nhiễm không khí đã tăng lên, đóng một vai trò quan trọng trong quản lý chất lượng không khí và ngăn chặn dân số chống lại ô nhiễm.
TỔNG QUAN VẤN ĐỀ NGHIÊN CỨU
Nghiên cứu nhằm mục đích xây dựng các mô hình dự báo chất lượng không khí hàng ngày ở một địa phương cụ thể, sử dụng một trong những phương pháp tiếp cận máy học (ML) mạnh mẽ nhất hiện có, cụ thể là, vectơ hỗ trợ (SVMs) và mạng noron nhân tạo (ANN).
Nhóm tác giả đưa ra đề xuất là xây dựng mô hình để dự đoán từng chất ô nhiễm và đo hạt trên cơ sở hàng ngày và dự đoán chỉ số chất lượng không khí hàng giờ (AQI) của một địa phương cụ thể.
Bài báo được tổ chức như sau. Phần 2, chúng tôi giới thiệu mô hình SVM và ANN. Phần 3, bao gồm mô tả về dữ liệu được sử dụng trong công việc này. Trong Phần 4, nhóm tác giả thảo luận thực nghiệm và so sánh kết quả. Phần 5 kết thúc bài báo và thảo luận về các ý tưởng cho nghiên cứu trong tương lai.
Trong bài báo này, nhóm tác giả dựa vào hai kỹ thuật học máy cơ bản được sử dụng trong nghiên cứu này Support Vector Machine(SVMs) và Artificial Neural Network (ANN).
Vectơ hỗ trợ (SVM) là mô hình học có giám sát, có thể được áp dụng để phân tích phân loại và phân tích hồi quy. Chúng đã được đề xuất bởi Vapnik vào năm 1995. Chúng có thể thực hiện cả nhiệm vụ phân loại tuyến tính và phi tuyến tính [2], [8], [9], [14].
Mạng thần kinh nhân tạo (ANN) là một mô hình tính toán cố gắng mô phỏng bản chất xử lý song song của não người. ANN là một mạng lưới các phần tử xử lý được kết nối chặt chẽ với nhau (tế bào thần kinh), hoạt động song song [8] lấy cảm hứng từ hệ thống thần kinh sinh học [13]. ANN được sử dụng rộng rãi trong nhiều nghiên cứu vì chúng có khả năng mô hình hóa các hệ thống phi tuyến tính, trong đó các mối quan hệ giữa các biến chưa biết là khá phức tạp [6]. Một ví dụ về ANN là Multi-Layer Perceptron (MLP), thường được hình thành từ ba lớp tế bào thần kinh (lớp đầu vào, lớp đầu ra và lớp ẩn) và các tế bào thần kinh của nó sử dụng các hàm phi tuyến để xử lý dữ liệu [7].
Support Vector Machine
Máy vectơ hỗ trợ (SVM) đã được giới thiệu trong [3], cho các bài toán phân loại. Mục tiêu là tìm kiếm siêu phẳng phân tách tối ưu giữa các lớp. Các điểm nằm trên ranh giới của các lớp được gọi là vectơ hỗ trợ và không gian ở giữa được gọi là siêu phẳng; khi một bộ phân tách tuyến tính không thể tìm ra giải pháp, các điểm dữ liệu được chiếu vào một không gian có chiều cao hơn, nơi các điểm phân tách phi tuyến trước đó trở thành có thể phân tách tuyến tính, sử dụng các hàm nhân. Toàn bộ nhiệm vụ có thể được xây dựng như một bài toán tối ưu hóa bậc hai có thể được giải quyết bằng các kỹ thuật chính xác.
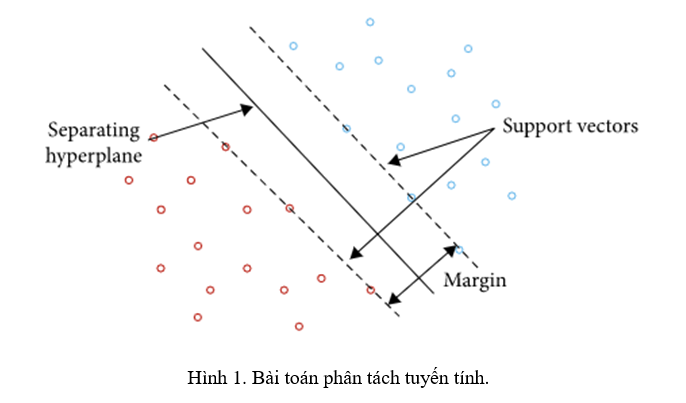
Cho tập dữ liệu đào tạo T, được đại diện bởi:Hình 1 trình bày một ví dụ về bài toán phân loại có thể phân tách tuyến tính được giải quyết bằng cách sử dụng máy vectơ hỗ trợ SVM. SVM nhằm mục đích tối đa hóa lợi nhuận giữa các vectơ hỗ trợ và siêu phẳng.Một năm sau khi giới thiệu SVM, Smola et al. [1] nâng cao một hàm mất mát thay thế, cũng cho phép SVM được áp dụng cho các bài toán hồi quy. Hồi quy vectơ hỗ trợ (Support vector regression – SVR) đã được áp dụng trong lĩnh vực dự báo, SVR là một phương pháp đầy hứa hẹn trong lĩnh vực dự báo, vì nó mang lại một số lợi thế: số lượng tham số ít hơn, khả năng dự báo tốt hơn và huấn luyện nhanh hơn.
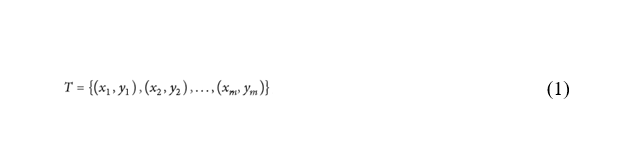
Trong đó x là đầu vào đào tạo và là đầu ra dự kiến đào tạo.
Một hàm phi tuyến:

Phương trình (2) có thể được viết lại thành một bài toán tối ưu hóa lồi có ràng buộc như sau:Trong đó w là vectơ trọng số, b là độ lệch, và Φ(xi) là không gian đặc trưng chiều cao, được ánh xạ tuyến tính từ không gian đầu vào x; mục tiêu là để phù hợp với tập dữ liệu huấn luyện T bằng cách tìm một hàm f(x) có độ lệch ε nhỏ nhất có thể so với các mục tiêu y.
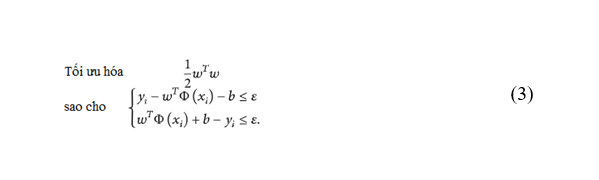
Mục đích của hàm mục tiêu được biểu diễn trong phương trình (3) là để tối thiểu hóa trong khi thỏa mãn các ràng buộc khác. Một giả thiết là tồn tại f(x), tức là bài toán tối ưu hóa lồi là khả thi. Giả định này không phải lúc nào cũng đúng; do đó, người ta có thể muốn đánh đổi sai số bằng tính ổn định của ước tính. Lưu ý điều này, Vapnik đã định dạng lại phương trình (3) dưới dạng:
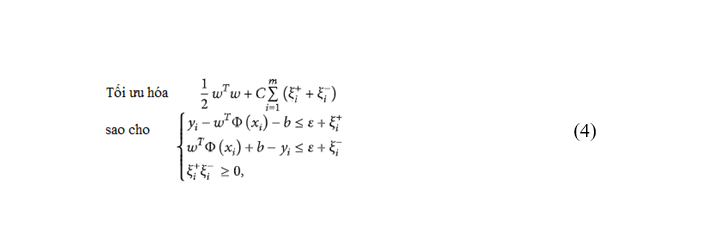
Để giải phương trình (4), có thể sử dụng số nhân Lagrang để loại bỏ một số biến cơ bản. Phương trình cuối cùng dịch bài toán tối ưu hóa kép của SVR là:Trong đó C <0 là một hằng số xác định trước chịu trách nhiệm điều hòa và đại diện cho trọng số của hàm mất mát. Số hạng đầu tiên của hàm mục tiêu wTw là thuật ngữ chính quy, trong khi số hạng thứ hai được gọi là thuật ngữ thực nghiệm và đo lường hàm mất mát ε.
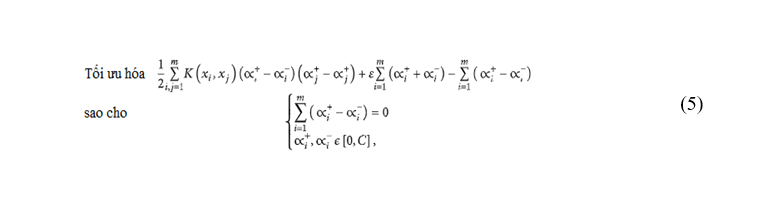
Hiệu suất và khả năng tổng quát tốt của SVR phụ thuộc vào ba thông số huấn luyện:Trong đó, K(xi, xj) là hàm nhân; công thức trên cho phép mở rộng SVR thành các hàm phi tuyến, vì hàm nhân cho phép xấp xỉ hàm phi tuyến trong khi vẫn duy trì tính đơn giản và hiệu quả tính toán của SVR tuyến tính.
- Hàm nhân
- C (tham số chính quy hóa)
- ε
Dưới đây là một số hàm nhân phổ biến được sử dụng:
 |
| Hàm |
Artificial Neural Network
ANN đa lớp được sử dụng để tạo các mô hình của trạng thái hệ thống bằng cách sử dụng kết hợp phi tuyến của các biến đầu vào (Bishop, 1995, Duda et al., 2001, Hastie et al., 2001). ANN được sử dụng trong nghiên cứu này là một mạng chuyển tiếp với các chức năng kích hoạt sigmoid trong các lớp ẩn và một chức năng kích hoạt tuyến tính trong nút đầu ra. Vì theo nghiên cứu của Bishop (1995), nhiều hơn một lớp ẩn thường không cần thiết, các kiến trúc của chúng ta chỉ có một lớp ẩn. ANN được đào tạo bằng cách sử dụng thuật toán lan truyền ngược với các thuật ngữ động lượng và giảm độ dốc.
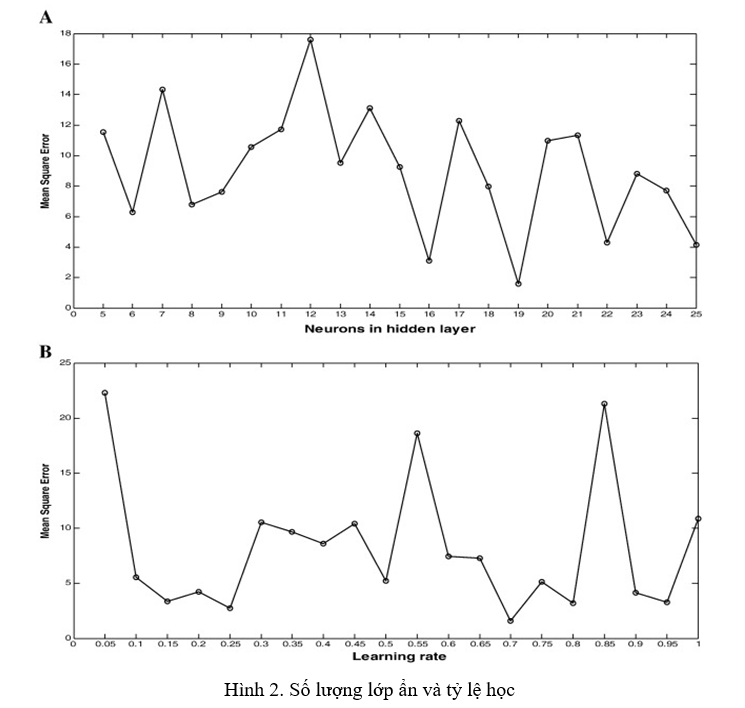
ANN yêu cầu rằng tốc độ học, số lượng nút trong một lớp ẩn duy nhất và số lần huấn luyện tối đa phải được chỉ định (Hill và Minsker, 2010). Trong bài báo này, chúng tôi sử dụng phương pháp sai số tối ưu. Số lượng nút trong lớp ẩn thay đổi trong khoảng từ 5 đến 23 và tỷ lệ học tập thay đổi từ 0,01 đến 1,0 với gia số 0,05. Đối với mỗi cấu hình, sai số bình phương trung bình (MSE) giữa đầu ra mô hình và dữ liệu đo được đã được tính toán. Hình 2 minh họa số lượng tế bào thần kinh tối ưu trong lớp ẩn và tốc độ học tập tối ưu có hiệu suất mô hình tối đa như được chỉ ra bởi MSE. Số lượng noron trong lớp ẩn và tốc độ học tối ưu được chọn bằng phương pháp thử-và-sai. Cấu trúc ANN cuối cùng có năm biến đầu vào với một nút chiếm độ lệch, 19 noron ẩn với một nút chiếm độ lệch, tốc độ học 0,7 và một biến đầu ra của lớp đầu ra (Hình 2, Hình 3).
Đối với mục đích dự đoán, thuộc tính quan trọng nhất của một mô hình là khả năng tổng quát hóa của nó. Trong khi khả năng tổng quát hóa chỉ ra sức mạnh của một mô hình để hoạt động tốt trên dữ liệu không được sử dụng để đào tạo nó, việc trang bị quá nhiều ngăn cản việc tổng quát hóa mô hình khi đối mặt với các tình huống mới (Schlink và cộng sự, 2003). Để tránh trang bị quá nhiều, việc ngừng sớm áp dụng kỹ thuật chính quy hóa thường được sử dụng nhất. Để áp dụng nó, tập dữ liệu được chia ngẫu nhiên thành hai tập, 80% dành cho đào tạo mô hình (để tính toán độ dốc và cập nhật các thông số mạng, chẳng hạn như trọng số và độ lệch – tập huấn luyện) và 20% để kiểm tra mô hình ( để kiểm tra xác thực lỗi mô hình – bộ xác nhận). Trọng số mô hình được khởi tạo ngẫu nhiên và quá trình huấn luyện bị dừng khi mạng bắt đầu trang bị quá nhiều dữ liệu, tức là lỗi trên tập hợp xác thực.
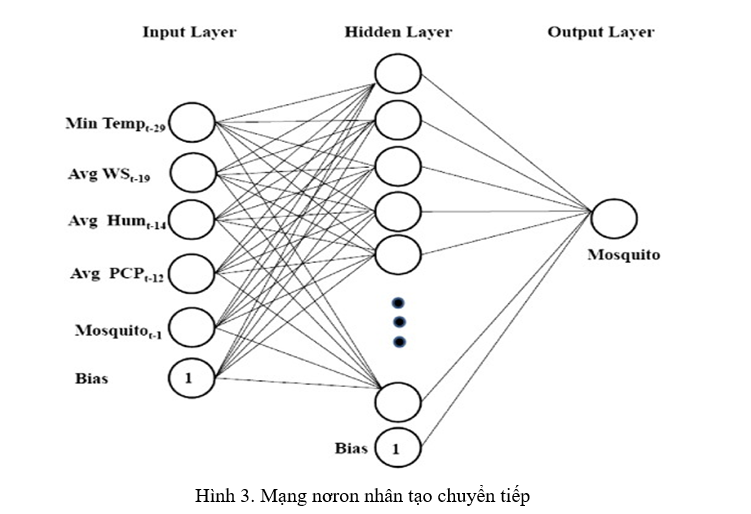
Để khảo sát khả năng giải thích của ANN, chúng tôi đã áp dụng các phân tích độ nhạy “trọng số” nói trên để xác định đóng góp tương đối và vai trò của các biến đầu vào trong hoạt động của muỗi (Garson, 1991, Song và cộng sự, 2013). Phương pháp trọng số được phát triển bởi Garson (1991). Tỷ lệ phần trăm ảnh hưởng của biến đầu vào lên giá trị đầu ra, Qik (%), cho biết tầm quan trọng của các biến đầu vào được xác định bởi:
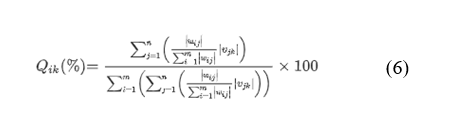
DỮ LIỆUTrong đó wij biểu thị trọng số giữa noron đầu vào i (= 1, 2,…, m) và nơ-ron ẩn j (= 1, 2,…, n) và vjk biểu thị trọng số giữa noron ẩn j và noron đầu ra k (= 1, 2,…, l)
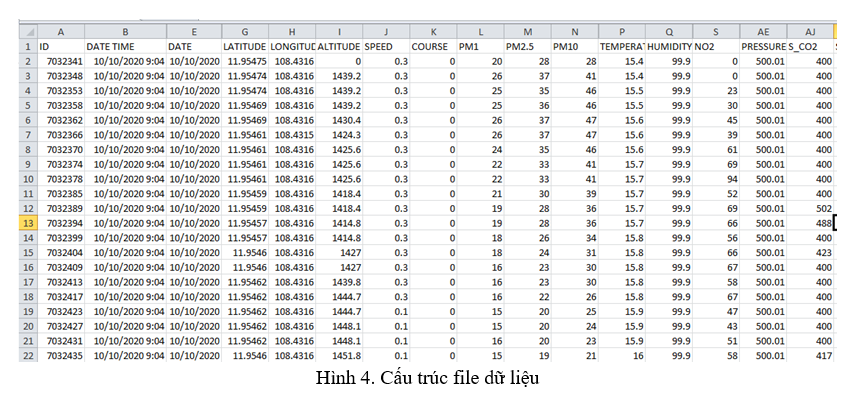
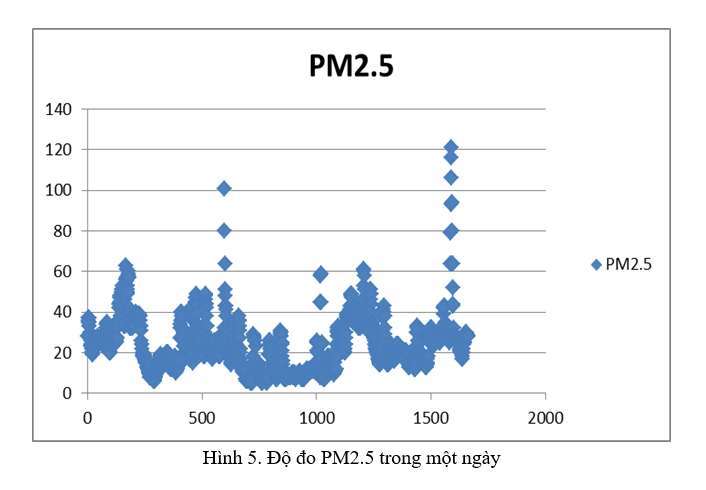
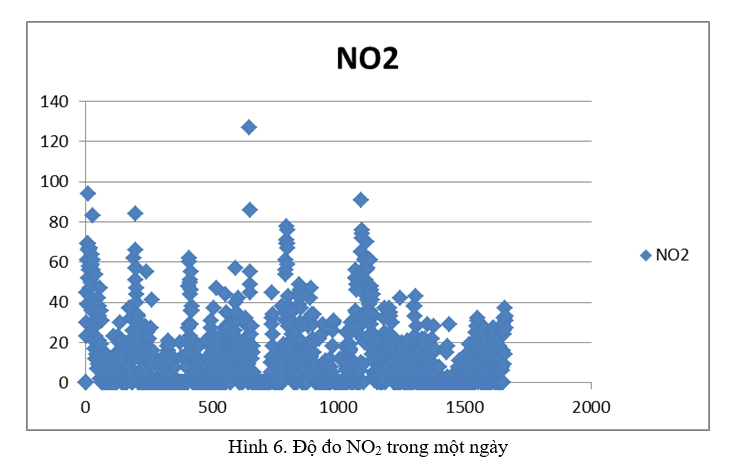
Bộ dữ liệu được sử dụng trong bài báo này được chúng tôi tiến hành thu thập tại một địa phương cụ thể (dữ liệu thực nghiệm tại thành phố Đà Lạt thuộc tỉnh Lâm Đồng) bằng thiết bị đo môi trường hỗ trợ bởi viện NICT Nhật Bản. Tất cả các tệp chứa dữ liệu hàng giờ, được phân tách bằng chất ô nhiễm hoặc thông số đang được đo – CO2, NO2, ozone, PM2.5, nhiệt độ, độ ẩm và gió, với ba quan sát cố định và hai quan sát di động. Các dữ liệu hàng giờ được thu thập từ ngày 01 tháng 01 năm 2020 đến ngày 30 tháng 11 năm 2020.
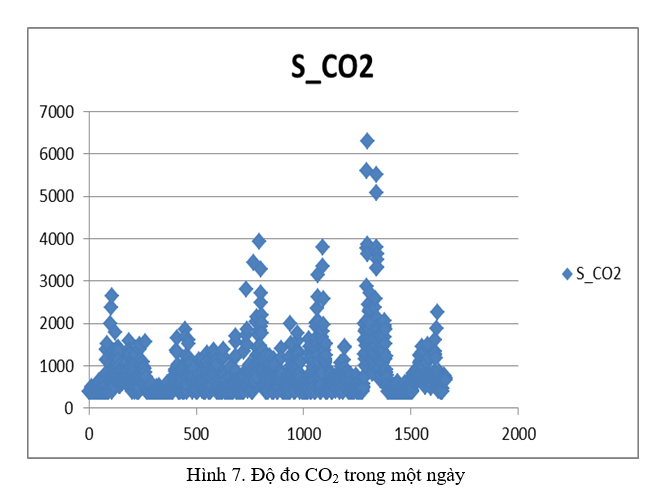
KẾT QUẢ NGHIÊN CỨU VÀ THỰC NGHIỆM
Trong bộ dữ liệu của chúng tôi, phần lớn dữ liệu bị thiếu có trong biến định tính cho tất cả các chất ô nhiễm, hạt và điều kiện khí tượng, tiếp theo là các phép đo mẫu CO2. Do số lượng lớn các giá trị bị thiếu cho các tính năng định tính chất ô nhiễm, hơn 70% tổng số các sự kiện có sẵn, nó đã được quyết định loại bỏ chúng khỏi tập dữ liệu. Đối với tất cả các biến phân loại khác, người ta quyết định điền các giá trị còn thiếu bằng giá trị phổ biến nhất từ mỗi đối tượng, như được đề xuất. Chúng tôi đã sử dụng ước lượng của đa thức bậc 2 để xử lý dữ liệu bị thiếu cho các biến số (CO2, SO2, NO2, PM2.5, nhiệt độ ngoài trời, độ ẩm tương đối và tốc độ gió). Phương pháp này đã được chấp nhận vì nó hoạt động tốt hơn so với cách áp đặt truyền thống hơn bằng cách sử dụng trung bình chuỗi hoặc nội suy tuyến tính.Chất lượng dữ liệu và tính đại diện của nó là những điểm đầu tiên và quan trọng nhất để đảm bảo việc xây dựng thành công các mô hình dự báo. Bước tiền xử lý dữ liệu thường tác động đến khả năng tổng quát hóa của thuật toán học máy. Tiền xử lý dữ liệu thường bao gồm việc nhập dữ liệu bị thiếu, loại bỏ hoặc sửa đổi các quan sát ngoại lệ, chuyển đổi dữ liệu (thường là chuẩn hóa và chuẩn hóa) và kỹ thuật tính năng. Trong khi hai bước đầu tiên hữu ích để có tập hợp dữ liệu chính xác và đầy đủ hơn, bước thứ ba thường được sử dụng để có dữ liệu được phân phối đồng đều hơn và giảm thiểu sự thay đổi dữ liệu. Cuối cùng, bước thứ tư được sử dụng để có được một tập dữ liệu mới, thường nhỏ hơn và nhiều thông tin hơn. Bước cuối cùng này thường bao gồm trích xuất đối tượng địa lý và lựa chọn đối tượng địa lý.
AQI là một chỉ số được các cơ quan chính phủ sử dụng để định lượng mức độ ô nhiễm của không khí. Theo EPA (Cơ quan Bảo vệ Môi trường Hoa Kỳ), giá trị AQI nằm trong khoảng từ 0 đến 500, khi AQI càng lớn thì ô nhiễm càng lớn. Giá trị AQI nên được hiểu theo phân loại được báo cáo trong Bảng 2.
 |
| Mức độ quan tâm đến sức khỏe |
Chỉ số AQI được tính theo công thức sau:
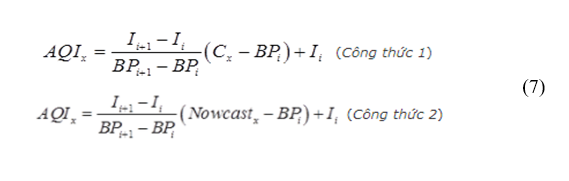
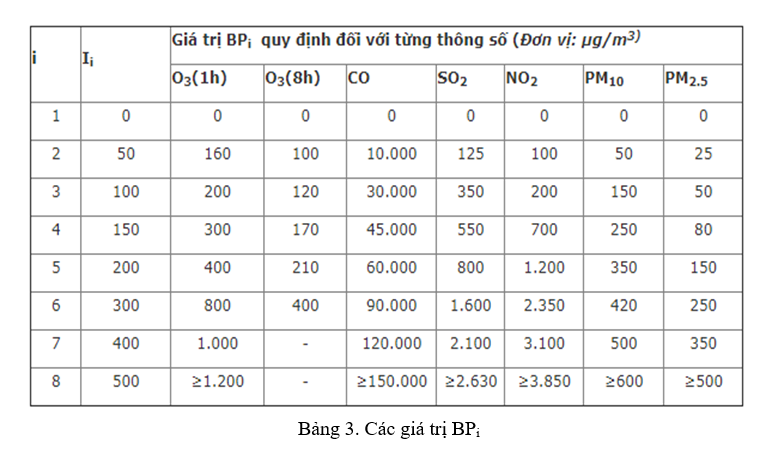
Trong đó, Các giá trị BPi đối với các thông số:
 |
| ANN |
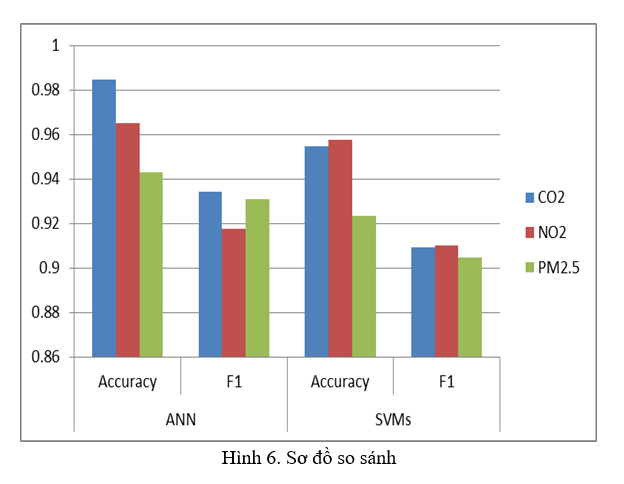
KẾT LUẬN
Dự báo chất lượng không khí là một công việc phức tạp do sự biến đổi lớn theo không gian và thời gian của các chất ô nhiễm và hạt. Đồng thời, khả năng lập mô hình, dự đoán và giám sát chất lượng không khí ngày càng trở nên quan trọng hơn, đặc biệt là ở các khu vực đô thị, đông dân cư, nhiều các nhà máy, do các tác động nghiêm trọng của ô nhiễm không khí đối với người dân và môi trường.
Trong nghiên cứu này, nhóm tác giả đã trình bày hai phương pháp học máy SVMs và ANN để dự báo mức độ ô nhiễm và hạt và xác định chính xác AQI. Phương pháp được nghiên cứu đã tạo ra một mô hình phù hợp về ô nhiễm khí quyển hàng ngày, cho phép chúng tôi có được độ chính xác tốt trong việc mô hình hóa nồng độ chất ô nhiễm như PM2.5, CO2 và NO2, cũng như AQI hàng giờ.
TÀI LIỆU THAM KHẢO
- A. Smola, C. Burges, H. Drucker et al., “Regression Estimation with Support Vector Learning Machines,” Technische Universität München, München, 1996. 14
- B. Holmes-gen and W. Barrett, Clean Air Future, Health and Climate Benefits of Zero Emission Vehicles, American Lung Association, Chicago, IL, USA, 2016. 5
- C. Cortes and V. Vapnik, “Support-vector networks,” Machine Learning, vol. 20, no. 3, pp. 273–297, 1995. 13
- D. Basak, S. Pal, and D. C. Patranabis, “Support vector regression,” Neuronal Information Processing-Letters and Reviews, vol. 11, no. 10, pp. 203–224, 2007. 16
- F. Caiazzo, A. Ashok, I. A. Waitz, S. H. L. Yim, and S. R. H. Barrett, “Air pollution and early deaths in the United States. Part I: quantifying the impact of major sectors in 2005,” Atmospheric Environment, vol. 79, pp. 198–208, 2013. 4
- G.Bontempi, S.Taieb, Y.Le Borgne, and D.Loshin, “Machine learning strategies for time series forecasting,” in Business Intelligence, pp. 59–73, Springer, Berlin, Germany, 2013. 8
- I. Alon, M. Qi, and R. J. Sadowski, “Forecasting aggregate retail sales:,” Journal of Retailing and Consumer Services, vol. 8, no. 3, pp. 147–156, 2001. 10
- J. C. M. Pires, M. C. M. Alvim–Ferraz, M. C. Pereira, and F. G. Martins, “Prediction of PM10 concentrations through multi-gene genetic programming,” Atmospheric Pollution Research, vol. 1, no. 4, pp. 305–310, 2010. 12
- L. A. Díaz-Robles, J. C. Ortega, J. S. Fu et al., “A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: the case of Temuco, Chile,” Atmospheric Environment, vol. 42, no. 35, pp. 8331–8340, 2008. 11
- L. Cao and F. Tay, “Financial forecasting using support vector machines,” Neural Computing & Applications, vol. 10, no. 2, 2001a. 15
- L. Pimpin, L. Retat, D. Fecht et al., “Estimating the costs of air pollution to the National Health Service and social care: an assessment and forecast up to 2035,” PLoS Medicine, vol. 15, no. 7, Article ID e1002602, pp. 1–16, 2018. 3
- R. G. Brereton and G. R. Lloyd, “Support vector machines for classification and regression,” The Analyst, vol. 135, no. 2, pp. 230–267, 2010. 17
- R. Sharda and R. B. Patil, “Neural networks as forecasting experts: an empirical test,” in Proceedings of the International Joint Conference on Neural Networks, pp. 491–494, San Diego, CA, USA, January 1990. 9
- T. M. Mitchell, “Machine learning,” in Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Pasadena, CA, USA, July 2009. 6
- U. A. Hvidtfeldt, M. Ketzel, M. Sørensen et al., “Evaluation of the Danish AirGIS air pollution modeling system against measured concentrations of PM2.5, PM10, and black carbon,” Environmental Epidemiology, vol. 2, no. 2, 2018. 1
- U. Brunelli, V. Piazza, L. Pignato, F. Sorbello, and S. Vitabile, “Three hours ahead prevision of SO2 pollutant concentration using an Elman neural based forecaster,” Building and Environment, vol. 43, no. 3, pp. 304–314, 2008. 7
- Y. Gonzalez, C. Carranza, M. Iniguez et al., “Inhaled air pollution particulate matter in alveolar macrophages alters local pro-inflammatory cytokine and peripheral IFN production in response to mycobacterium tuberculosis,” American Journal of Respiratory and Critical Care Medicine, vol. 195, p. S29, 2017. 2
Lê Đăng Nguyên và CS
Các tin khác

Bệnh viện Trung ương Huế với việc chăm sóc sức khỏe phụ nữ khu vực Miền Trung-Tây Nguyên

Chương trình nghệ thuật đặc biệt mừng 50 năm non sông thống nhất

Di tích Quốc gia đặc biệt Tây Thiên điểm đến du xuân bái phật hàng đầu miền Bắc

Đất Thạch Thố và men Thiên Hà tạo nên Tinh hoa Gốm Việt

Lưu giữ, lan tỏa tinh hoa đúc trống đồng Đông Sơn

Đến với vẻ đẹp bí ẩn hoang sơ của Vân Nam

Môi sinh tịnh độ ngay tại nhân gian

Tĩnh là trí tuệ

Chương trình nghệ thuật chào mừng những du khách đầu tiên tới Sa Pa năm 2025
Đọc nhiều

Nghiên cứu ứng dụng D-Panthenol và hệ nền sinh học: Bước tiến mới của DUYENTHI GROUP trong phục hồi hàng rào bảo vệ da

Những kỳ tích y khoa đầu năm 2026 tại Bệnh viên Đa khoa vùng Tây Nguyên

Mega Sale 2026 lan tỏa xu hướng tiêu dùng xanh tại Cần Thơ

Cần Thơ xây dựng đội ngũ cán bộ y tế “Giỏi chuyên môn, sáng y đức, vững bản lĩnh, tận tâm phục vụ”

Quản lý đau hiệu quả, thước đo chất lượng chăm sóc người bệnh
Videos
E-magazine Inforgraphic Video

Thủ tướng động viên lực lượng bảo đảm vệ sinh môi trường ở Hà Nội

Diễn văn của Tổng Bí thư Tô Lâm tại phiên bế mạc Đại hội XIV của Đảng

Đại hội XIV của Đảng sự kiện trọng đại của đất nước trong giai đoạn mới

Hợp tác xã bệ đỡ vùng trồng rau an toàn tập trung tại Hưng Yên

Hưng Yên sản xuất rau quả công nghệ cao hướng đi bền vững cho nông nghiệp sạch

Xã Ô Diên – Hà Nội: Bất cập từ bãi vật liệu xây dựng gây ô nhiễm môi trường và trách nhiệm quản lý tại địa bàn cơ sở

Cảnh báo hành vi giả danh cán bộ thuế, cơ quan thuế để lừa đảo
Phòng ngừa cháy nổ trong dịp Tết Nguyên đán

Thủ tướng Phạm Minh Chính gửi thư chúc mừng Đội tuyển bóng đá nam U23 Việt Nam

Thể thao Phú Thọ khẳng định vị thế mới - bước tiến từ thành tích đến sức hút những sự kiện lớn

Khai mạc giải Vô địch các câu lạc bộ Kickboxing toàn quốc năm 2025

Herbalife Việt Nam tiếp tục đồng hành hỗ trợ bữa ăn dinh dưỡng cho hơn 3.000 người có hoàn cảnh khó khăn
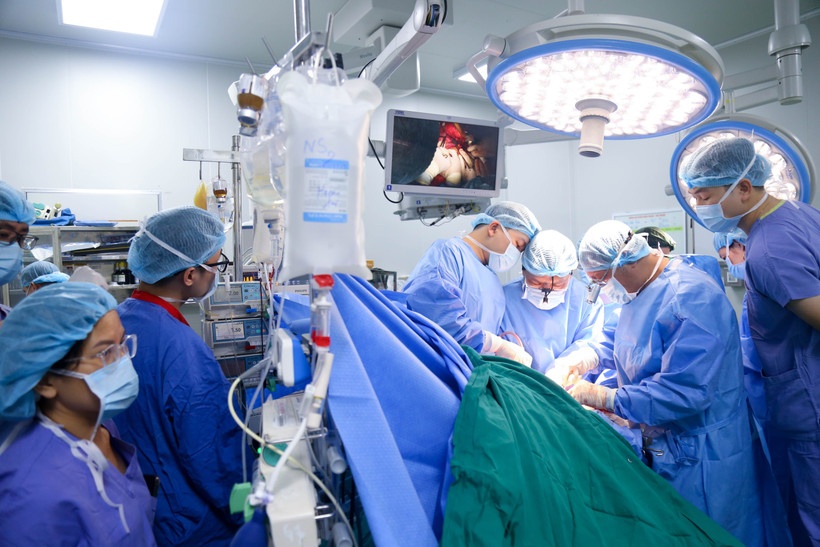
Chàng trai 21 tuổi hiến tạng sau chết não, hồi sinh bốn cuộc đời

XLIII Coffee Hà Nội - "Viên ngọc ẩn" trên phố Quang Trung với trải nghiệm cà phê đẳng cấp

Prudential thúc đẩy chăm sóc sức khỏe chủ động qua chương trình “Sống chủ động – Đẩy lùi ung thư vú”

Các Đoàn Kinh tế-Quốc phòng Quân khu 9: Làm tốt chức năng chiến đấu, công tác, lao động sản xuất
Nổi bật

Tuyên Quang: Bí thư Tỉnh ủy Hầu A Lềnh dự Lễ giao nhận quân năm 2026

Phú Thọ: Hàng vạn du khách tham dự lễ hội chọi trâu xã Hải Lựu năm 2026

Bầu cử sớm tại khu vực cụm Ba Kè ngoài khơi vùng biển Việt Nam

Sa Pa (Lào Cai): Đêm thơ Nguyên tiêu Xuân Bình Ngọ 2026 thu hút đông đảo các văn, nghệ sĩ, những người yêu thơ tham gia

Ứng cử viên đại biểu Quốc hội khóa XVI tiếp xúc cử tri phường Điện Biên Phủ

Hơn 30 chuyên gia từ Mỹ và Anh khám từ thiện cho bệnh nhân nghèo

TTYT huyện Yên Lạc: Đẩy mạnh cải cách hành chính hướng tới sự hài lòng người bệnh
Bệnh viện C Thái Nguyên: Nghiên cứu và ứng dụng khoa học, kỹ thuật trong công tác khám, chữa bệnh

Bệnh viện Lao và bệnh Phổi Thái Nguyên nỗ lực vượt mọi khó khăn trong khám và điều trị bệnh

Trung tâm Y tế thị xã Phổ Yên: Nơi người bệnh gửi gắm niềm tin

Bệnh viện A Thái Nguyên: Nỗ lực, cống hiến, vì sức khỏe nhân dân

Trung tâm y tế huyện Đồng Hỷ: Nâng cao chất lượng chăm sóc và bảo vệ sức khỏe nhân dân
Trung tâm Y tế Chợ Đồn (Bắc Kạn): Không ngừng đổi mới, nâng cao chất lượng khám chữa bệnh